Existen varias conexiones que se pueden dar entre las Matemáticas y la Estadística. Una de ellas la describe Jhon Cook en su blog, sobre una relación existente entre la probabilidad y la geometría. Más específicamente entre las desviaciones estándar entre variables independientes y el Teorema de Pitagoras, la correlación entre variables aleatorias dependientes y la ley de cosenos. Esto debe ser que la correlación es un coseno según Cook.
A continuación vamos a describir la relación que se encuentran.
Variables independientes
En primer lugar, vamos a empezar con dos variables aleatorias independientes \(X\) e \(Y\). Las desviaciones estándar de \(X\) e \(Y\) son tomadas como los lados de un triángulo rectángulo (ver Figura 1)
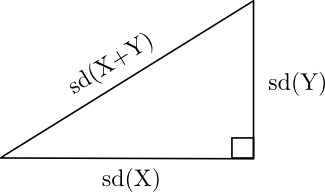
En la Figura 1, la Desviación Estándar (\(sd\)) es la raíz cuadrada de la varianza. La figura nos indica que la fórmula de la Varianza es
\[\text{Var}(X+Y) = \text{Var}(X) + \text{Var}(Y)\]
el cual la formula es análoga al Teorema de Pitágoras
\[c^2 = a^2 + b^2.\]
Variables dependientes
Ahora supongamos que las variables son dependientes. Si \(X\) e \(Y\) están correlacionadas, la fórmula de la varianza es análoga a la ley de los cosenos (ver Figura 2).
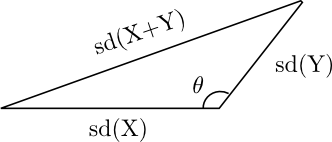
La generalización de la fórmula anterior para la varianza entre variables dependientes es
\[\text{Var}(X+Y) = \text{Var}(X) + \text{Var}(Y) + 2\text{Cov}(X, Y).\]
\(\text{Cov}(X, Y)\) es la covarianza de \(X\) e \(Y\). La ley de los cosenos es análoga
\[c^2=a^2+b^2-2ab\cos(\theta).\]
\(a\), \(b\) y \(c\) son las Desviaciones Estándar de \(X\), \(Y\) y \(X +Y\), respectivamente, entonces el \(\cos (\theta) =-\rho\) donde \(\rho\) es la correlación entre \(X\) e \(Y\) se define como
\[\rho(X,Y)=\frac{\text{Cov}(X,Y)}{\text{Sd}(X)\text{Sd}(Y)}.\]
Cuando \(\theta\) es \(\pi/2\) las variables aleatorias son independientes. Cuando \(\theta\) es mayor, las variables se correlacionan positivamente. Cuando \(\theta\) es menor, las variables tienen una correlación negativa. Dicho de otra manera, como \(\theta\) aumenta de \(0\) a \(\pi\), los aumentos de correlación \(-1\) a \(1\).
La analogía anterior es un poco torpe, debido al signo menos.Reformulemos la formula anterior utilizando el ángulo suplementario \(\varphi =\pi-\theta\). Deslice la línea que representa la desviación estándar de \(Y\) sobre el extremo izquierdo de la línea horizontal que representa la desviación típica de \(X\) (Ver Figura 3).
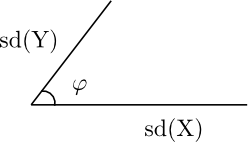
El \(\cos(\varphi) =\rho=\text{Corr} (X, Y)\).
Cuando \(\varphi\) es pequeño, los dos segmentos de línea están apuntando en casi la misma dirección y las variables aleatorias son altamente correlacionados positivamente. Si \(\varphi\) es grande, cerca a \(\pi\), los dos segmentos de línea están apuntando en direcciones opuestas y cerca de las variables aleatorias son altamente correlacionados negativamente.
Explicación de la conexión
El origen de la conexión entre la correlación y el teorema del coseno esta en el espacio producto entre \(X\) e \(Y\) el cual el producto interno \(\langle X,Y\rangle\) estadísticamente es \(\text{E} (XY)\). Entonces
\[\langle X+Y, X+Y\rangle=\langle X,X\rangle +\langle Y,Y\rangle +2\langle X,Y\rangle.\]
En un espacio con producto interno,
\[\langle X,Y\rangle=\left \| X \right\|\left\| Y \right\|\cos\varphi ,\]
donde la norma de un vector \(\left\| X \right\|\) es la raíz cuadrada del producto escalar del vector por sí mismo. La ecuación anterior define el \(\varphi\) ángulo entre dos vectores. Se podría justificar esta definición al ver que está de acuerdo con la geometría plano ordinario en el plano que contiene los tres vectores \(X\), \(Y\) y \(X + Y\).
Ver también: Teorema del Límite Central.
No hay comentarios:
Publicar un comentario